Session 5

1 Graphs

1.1 Exercise

1) Which of the following graphs are isomorphic (i.e. they are the same but their layout is different)?

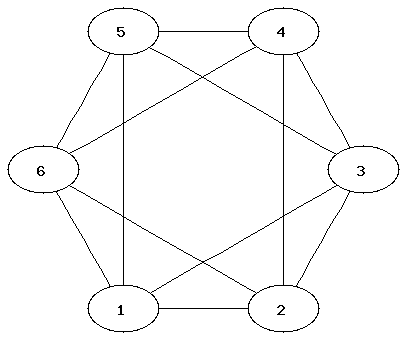
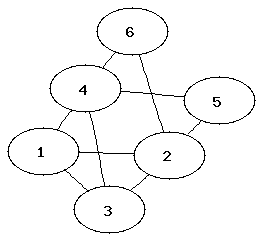
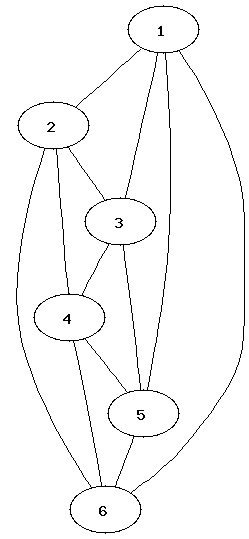
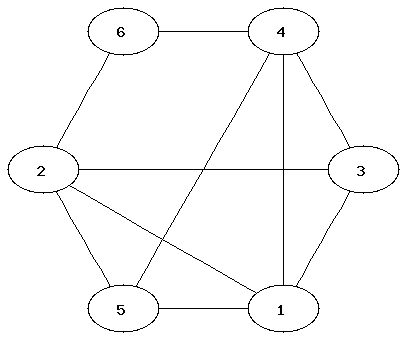
1:
2:
3:

4:
5:
6:

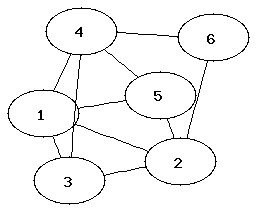
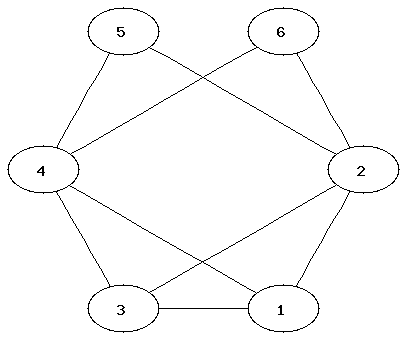
It can be easier to determine that two graphs are not isomorphic than to show that they are. Which property of the nodes can be used to determine that two graphs are not isomorphic?

1.2 Creating graphs with NetworkX

In order to use the graph modules, the following is needed:

sys.path.append('/home/cs170/networkx/')
from networkx import *

Commands for creating a graph and adding nodes and edges:

G=Graph()                           ### initialises a new graph
G.add_node("One")
G.add_nodes_from(["Hello","World"]) ### adding a list of nodes
G.add_edge("Hello","World")
G.add_edges_from([("One","Hello"),("One","World")])
H= DiGraph(G)                       ### creates a directed graph using G
G.clear()                           ### removes all nodes and edges from a graph

Commands for displaying nodes and edges:

G.nodes()
G.edges()

1.3 Exercise

2) Create Graph 1 from exercise 1).

1.4 Viewing graphs

The following command creates a gif file of a graph G:

write_gif(G,"filename")

Instead of filename you should type a name of a file (without extension). After executing the command, two files, filename.gif and filename.dot (which can be ignored), will appear in the current directory. You can view the gif file via your I:-drive.

The software that creates the layouts is called Graphviz. These layout options are available:

write_gif(G,"filename") hierarchical layout
write_gif(G,"filename","neato") spring model layout
write_gif(G,"filename","fdp") another spring model layout
write_gif(G,"filename","twopi") radial layout
write_gif(G,"filename","circo") circular layout

This website has more information about Graphviz and the different types of layouts.

(Note: the write_gif function is only available on DCS. Here is information on how to use Graphviz on other computers.)

1.5 Exercises

3) Try different layouts for the graph you created in exercise 2.

4) NetworkX provides many standard graphs. Try different layouts for these:

G1=house_x_graph()
G2=complete_bipartite_graph(3,5)
G3=lollipop_graph(10,20)

Where did you see the House Graph in the lecture?

1.6 Exercises: other graph operations

5) NetworkX provides many graph operations. Using the graphs G (from exercise 2) and G1, G2, G3 from exercise 4 determine the following:

Which of the graphs are bipartite (using is_bipartite(G)?
Generate the complement of G1 (using complement(G1). Look at the gif files for G1 and its complement. Can you figure out what is meant by "complement" here?
Calculate the diameter(G) and the radius(G) of the graphs. The diameter is the maximum distance (shortest path) between two nodes in the graph; the radius is the minimum steps needed to reach all nodes from a single node. How much larger can the diameter be compared to the radius? Can you use these values to determine which of the graphs have a small-world effect with "six degrees of separation"?

1.7 Exercises with pen and paper

Using the graphs from exercise 1 and G1, G2, G3 from exercise 4 determine the following:

6) Determine the chromatic number of the graphs. (The chromatic number is the minimum number of colours needed to colour a graph so that neighbouring nodes have different colours.)

7) Which of the graphs have a Hamiltonian or Eulerian path?

write_gif(G,"filename")	hierarchical layout
write_gif(G,"filename","neato")	spring model layout
write_gif(G,"filename","fdp")	another spring model layout
write_gif(G,"filename","twopi")	radial layout
write_gif(G,"filename","circo")	circular layout